Численное решение обыкновенных дифференциальных уравнений (ОДУ) в Python

Рассмотрены приемы решения обыкновенных дифференциальных уравнений (ОДУ) с помощью модуля scipy.integrate языка Python

Краткое описание модуля scipy.integrate

Модуль scipy.integrate имеет две функции ode() и odeint(), которые предназначены для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (т.е. задача Коши).

Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.

from scipy.integrate import odeint

Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат

odeint(func, y0, t[,args=(), ...])

Решение одного ОДУ

Допустим надо решить диф. уравнение 1-го порядка

Код программы:

import numpy as np
from scipy. integrate import odeint
import matplotlib.pyplot as plt

 # create function
def dydt(y, t):
	return -y*t

t = np.linspace( -2, 2, 51) # vector of time
y0 = 1 # start value
y = odeint (dydt, y0, t) # solve eq.
y = np.array(y).flatten() 
plt.plot( t, y,'-sr', linewidth=3) # graphic
plt.show() # display

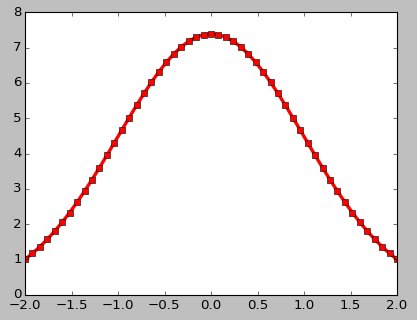
Получилось что-то такое:

Решение системы ОДУ

Пусть теперь мы хотим решить (автономную) систему диф. уравнений 1-го порядка

import numpy as np
from scipy. integrate import odeint
import matplotlib.pyplot as plt

 # create function
def f(y, t):
	y1, y2 = y
	return [y2, - y2 - y1]

t = np.linspace( 0, 10, 41) # vector of time
y0 = [0, 1] # start value
w = odeint(f, y0, t) # solve eq.
y1 = w[:,0]
y2 = w[:,1]
fig = plt.figure(facecolor='white')
plt.plot(t, y1, '-o', t, y2, '-o', linewidth=2)
plt.ylabel("z")
plt.xlabel("t")
plt.grid(True)
plt.show() # display

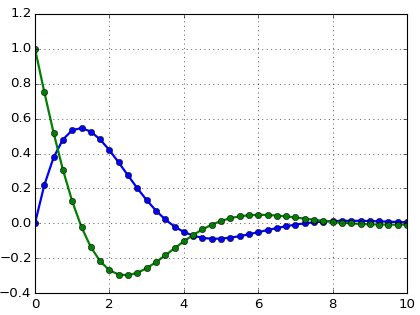
Выходной массив w состоит из двух столбцов - y1(t) и y2(t).

Результат работы:

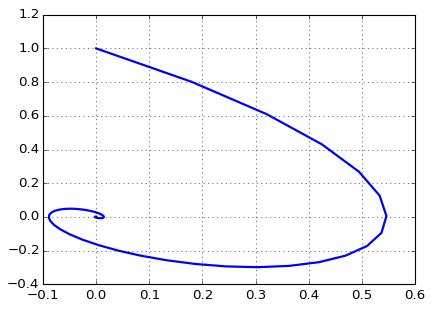
Также без труда можно построить фазовые траектории:

fig2 = plt.figure(facecolor='white')
plt.plot(y1, y2, linewidth=2)
plt.grid(True)
plt.show()